一、几何知识
1.1 判断点与直线的关系
向量叉乘
已知直线上两点p1(x1,y1), p2(x2,y2),测试点t(x,y),设p1,p2所在的向量为v1, p1t所在的向量为v2。则可以通过v1 x v2来判断点t与直线p1、p2的关系。当:
v1 x v2 > 0 :v2在v1逆时针方向(左侧)
v1 x v2 < 0 :v2在v1顺时针方向(右侧)
v1 x v2 = 0 :v2与v1平行(由于起点相同,v1、v2共线)解直线方程
已知直线上的两点p1(x1,y1) p2(x2,y2), p1 p2两点不重合。则直线的一般式方程AX+BY+C=0,结合两点式可得出,其中A B C分别为:
A = y2-y1;
B = x1-x2;
C = x2 * y1-x1 * y2
把测试点t(x, y)代入直线方程得:
D = Ax + By + C
若 D > 0 则t在直线右侧
若 D < 0 则t在直线左侧
若 D = 0 则t在直线上
参考1
参考2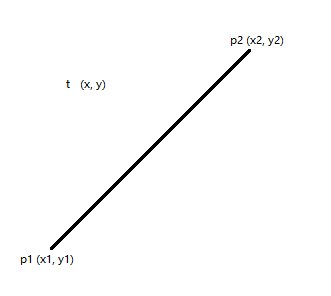
1.2 两条直线的交点
求两条直线的交点方式很多,比如:解联立方程、投影法、面积法、解参数方程。这里介绍参数方程求两条直线的交点,参数方程需要求两条线段向量的叉乘,而我们可以通过叉乘预先排除两条直线平行的情况。
假设线段L1的两个端点为s1, e1; L2的两个端点为s2, e2,则向量L1,L2可表示为:
V1 = e1 - s1
V2 = e2 - s2
参数方程可表示为:
x = s1 + t V1
y = s2 + u V2
若两条直线相交,则:
s1 + t V1 = s2 + u V2
两边同时叉乘法 V2得:
s1 x V2 + t V1 x V2 = s2 x V2 + u V2 x V2
根据叉乘的几何意义,可知:V2 x V2 = 0
t = (s2 - s1) x V2 / (V1 x V2)
同理可得
u = (s1 - s2) x V1 / (V2 x V1)
因为 P x Q = - (Q x P) 所以
u = V1 x (s1 - s2) / (V1 x V2) (转换的目的是为了算法效率,V1xV2一般在预判断两直线是否相交时,就会计算)
当 0 <= t <= 1,且 0 <= u <= 1时,两线段相交
把t、u分别代入参数方程中即可得到交点
s1 + t V1
参考1
参考2
1.3 三角形的外接圆
三角形外接圆的圆心(外心)为三条边垂直平分线的交点,已知三角形的三个顶点坐标,求三角形外心可以通过下面2种方法求得:
1.点法式解连立方程:已知两点可求出方向向量和法向量,根据两点的中点和法向量可用点法式表示出直线A,再取另外两点计算法向量和中点代入点法式可得直线B,直线A、B角连立方程可得交点(圆心),圆心到三角形任意一点的距离即半径。
2.圆心到三个顶点距离等于半径:设点C(x,y)为圆心,CA、CB、CC的距离为半径,解方程可得圆心。
参考
二、 根据点集生成三角形
本文讨论基于三角形的navmesh寻路,在地图编辑器中,各种态静态阻挡可以通过点线构成,在地图器中编辑完静态阻挡后,需要把可行走区域三角形化,以便于寻路。Delaunay三角剖分能够构造出一张良好三角形网,网中的三角形具有如下特性:
- 最接近:以最接近的三点形成三角形,且各线段(三角行的边)皆不相交。
- 唯一性:不论从区域何处开始构建,最终都将得到一致的结果。
- 最优性:任意两个相邻三角形构成的凸四边形的对角线如何可以互换的话,那么两个三角形六个内角中最小角度不会变化。
- 最规则:如果将三角网中的每个三角形的最小角进行升序排列,则Delaunay三角网的排列得到的数值最大。
- 区域性:新增、删除、移动某一个顶点只会影响邻近的三角形。
- 具有凸边形的外壳:三角网最外层的边界形成一个凸多边形的外壳。
- 能够使生成的三角形中最小角最大化
1.1 Delaunay三角剖分算法
Delaunay三角剖分算法非常多,比如分治算法系列、逐点算法系列、三角网生成法系列,本文使用的方法来自论文 原文 (密码:MbQp)算法步骤如下:
Step1.建立单元大小为 E × E 的均匀网格, 并将多边形域的顶点和边放入其中。其中 E = sqrt((bw ×bh)/n) , bw 和 bh分别为多边形域包围盒的宽度、高度, n为多边形域的顶点数。
Step2.取任意一条外边界边 p1 p2。
Step3.计算 DT 点 p3 , 构成约 束 Delaunay 三角形p1 p2 p3。
Step4.如果新生成的边 p1 p3 不是约束边, 若已经在堆栈中, 则将其从中删除;否则, 将其放入堆栈;类似地, 可处理 p3 p2。
Step5.若堆栈不空, 则从中取出一条边, 转 Step3;否则, 算法停止。
1.2 确定 DT 点
对于均匀网格上的任意一条线段 p1 p2 ,将其最小包围盒 Bm(p1 p2)内(包含相交)的网格单元构成 的包围盒称为 p1 p2 的网格包围盒。 确定 DT 点的过程如下 :
Step1.构造三角形p1 p2 p3 的外接圆 C(p1, p2, p3)及其网格包围盒 B(C(p1, p2, p3))。
Step2.依次访问网格包围盒内的每个网格单元: 对未作当前趟数标记的网格单元进行搜索, 并将其标记为当前趟数。若某个网格单元中存在可见点 p 并且∠p1 p p2 > ∠p 1 p3 p2 , 则令p3 = p , 转Step1; 否则, 转 Step3。
Step3.若当前网格包围盒内所有网格单元都已被标记为当前趟数, 也即 C(p1, p2, p3)内无可见点, 则 p3 为 p1 p2 的 DT 点。
1.3 可见点
我们称 p3 为 p1 p2 的可见点, 其必须满足下面 三个条件 :
(1)p3 在边 p 1 p2 的左侧;
(2)p3 与 p1 可见, 即对于 p1p3 所穿过的所有网格单元中记录的任意一条边 e ,有 e ∩(p1 p3)=φ ;
(3)p3 与 p2 可见。
参考 (密码:MbQp)
三、基于三角形的A*寻路算法
1.1 基本思想
在基于正方形格子的A* 算法中,给出任意一个格子可以很方便找出与之相邻所有格子,但基于三角形格子并不能通过坐标找出与之相邻的三角形。所以需要对生成的三角形做预处理,这里采用邻接表保存每个三角形相邻的三角形。与正方开格子不同的是,公式F=G+H中的G值为穿入边中点和穿出边中点连线的距离。其余步骤和A* 一样。
参考
1.2 拐点计算
用A*算法寻出来的路径可能是如下所示的一条很绕的路径,但是游戏中,我们理想的效果是尽量走直线,直线不能达的再通过拐点到达。
- 思路:
设:起点A到第一条穿出边的b点所构成的向量为:VLeft(A,b)
起点A到第一条穿出边的a点所构成的向量为:VRight(A,a)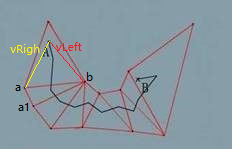
具体方法如下:
- 判断下一条穿出边的端点b1(这里b1即b)是否在vLeft与vRight之间,若在则更新vLeft(A,b)为vLeft(A, b1), 否则不更新。
- 判断下一条穿出边的端点a1否在vLeft与vRight之间,若在则更新vRight(A,a)为vRight(A, a1), 否则不更新。
- 只要任意一点更新,则会继续判断下一条边。
- 若下一穿出边的2个端点都不在vLeft(An, bn)和vRight(An, an)之间,若在vLeft(An,bn)左侧,则bn为拐点;若在vRight(An, an)右侧,则an为拐点。
- 重复1 ~ 4直到最后一条穿出边。

终点的处理:
设最后一条穿出边的两个端点分别为p1、p2,上个拐点为P, 若终点不在VLeft(P,p1)与VRight(P,p2)之间,则需要在p1或p2处添加拐点。
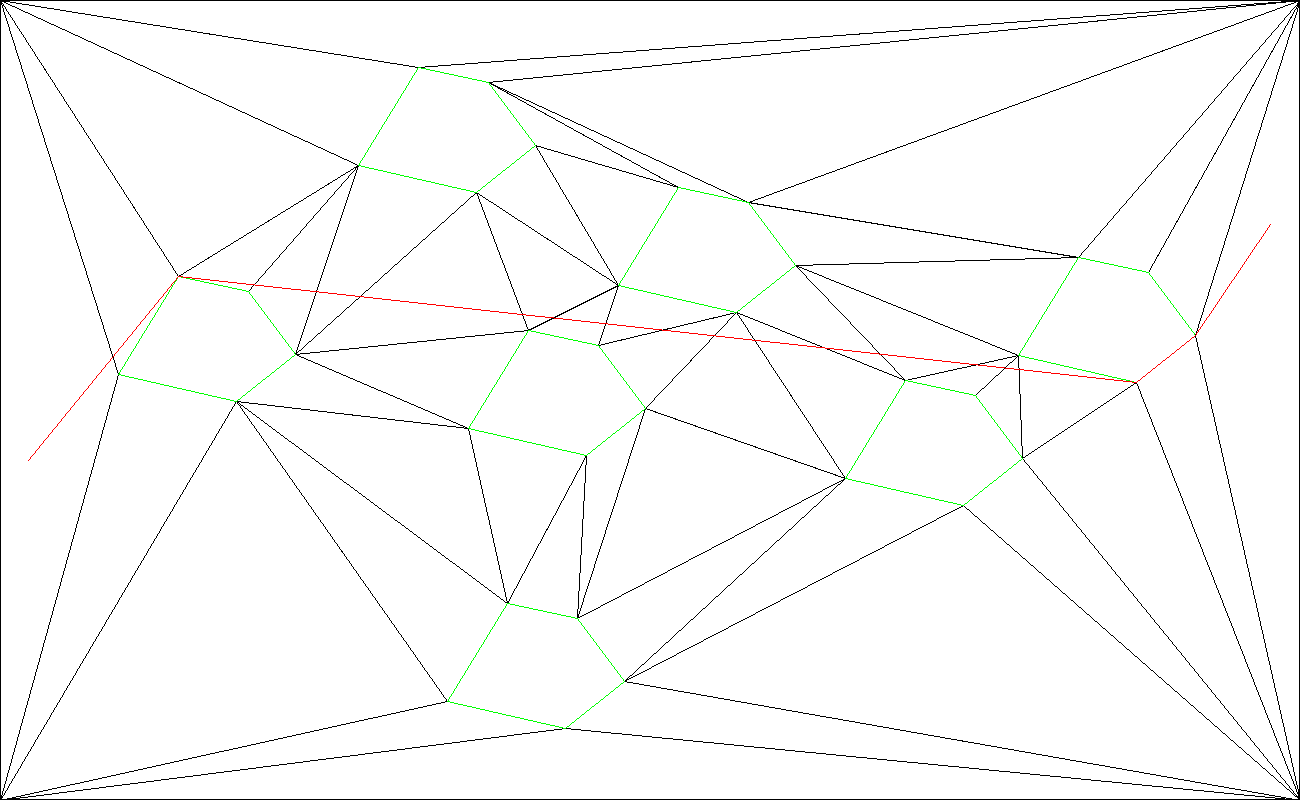
下图是一个基于三角形的mesh寻路结果:绿色边框为阻档,红色线为角色行走路径。