本文介绍2种常用的AOE技能目标选择器实现方法，矩形区域和扇形区域。
一、矩形区域
有技能描述是“对长距离路径上的敌人造成伤害，并给予状态5秒”。长距离路径上的敌人其实就是施法者到直接目标之间所构成矩形区域中的敌人。这个需求可以化成判断点是否在矩形区域内。如下图所示：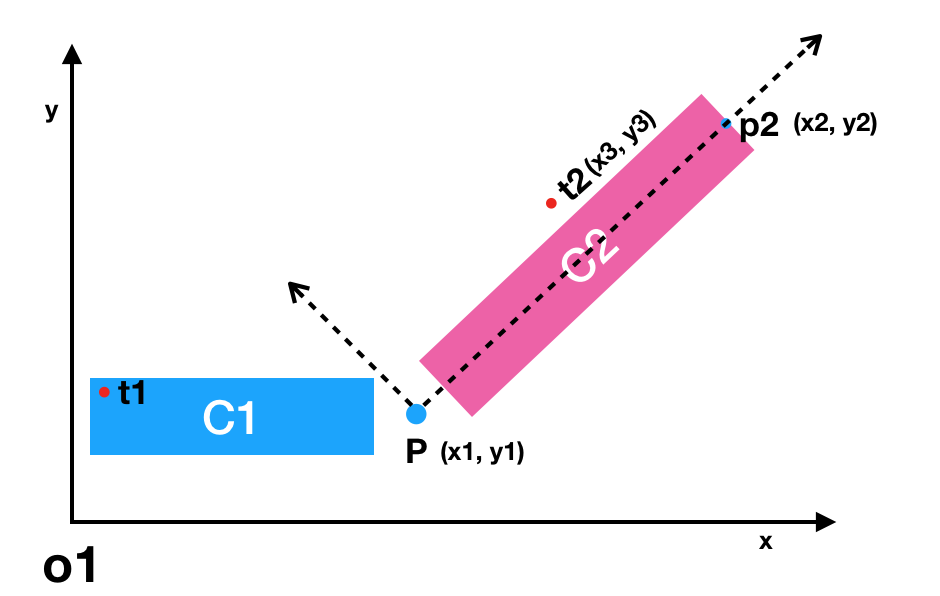
如何判断点在矩形内呢？
如上图所示c1为蓝色区域矩形，t1为矩形中的一个点
最简单的方法是判断t1.x >= min(c1.x) && t1.x <= max(c1.x) && t1.y >= min(c1.y) && t1.y <= max(c1.y)为true则点在矩形内，否则在矩形外。但是这种方法只有在矩形平行坐标轴时成立，如果攻击者方向不平行坐标轴如图中C2。我们用上面的方法计算时t2与矩形C2的位置关系时，发现它在矩形中，这显然不正确。那该如何计算t2与矩形C2的位置关系呢?
如果把施法者p到受击者p2之间的向量看成是新的x轴方向（虚线所示的相对坐标系），则被测试点与矩形的关系就可以用上术方法来判断。下面介绍如何把t2的坐标转换到pp2为x轴的相对坐标。
思路：通过求出被测点t2的极坐标，再通过极坐标转直角坐标就得到了t2的相对坐标，如下：
极坐标定义：该坐标系中任意位置可由一个夹角和一段相对原点(极点)的距离来表示，例如pt可以表示为(|pt|, t2pp2度数)
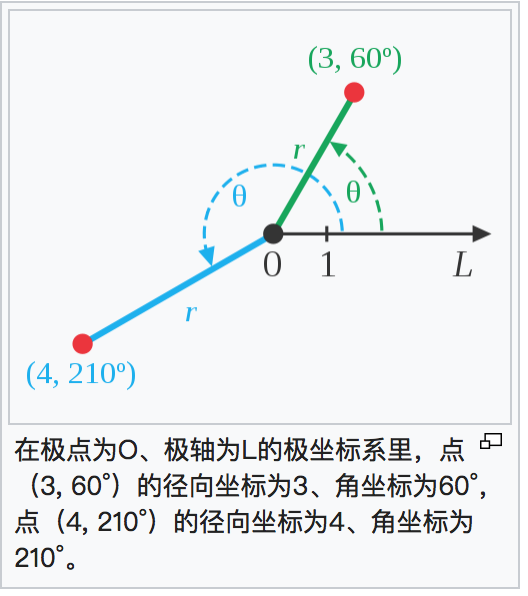在本例中，已知p和t2的坐标，则|pt2|的值为径向坐标；因为已知三角形pt2p2的三边，根据余弦定理可求出角t2pp2的角度，即极坐标的角坐标
根据余弦定理：
a^2 = b^2 + c^2 - 2bccosθ
得：cosθ = b^2 + c^2 - a^2 / 2bc
其中：a为t2p2, b为pt2, c为pp2,θ为角t2pp2
根据极坐标与直角坐标转换公式可得：
假设t2的相对坐标为(tr.x, tr.y)则
tr.x = pt2costθtr.y = sqrt(pt2^2 - tr.x^2)
注：pt2就是公式中的ρ
知道相对坐标，用平行坐标轴的算法很容易求出点是否是矩形内。
二、扇形区域
判断点是否在扇形中的方法很多，本文介绍通过点积来判断:
点积代数定义：a·b = a.x * b.x + a.y * b.y
点积几何定义：a·b = |a||b|cosθ (θ为ab之前的夹角)
如下图所行，u为施法者朝向，t为被攻击者坐标，θ为扇形角度的1/2, 下面我们要判断点t是否在扇形区域内。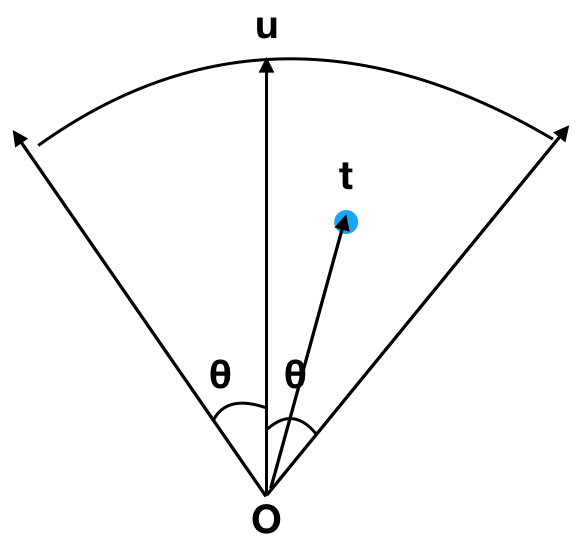
步骤：
- 首先判断ot的距离是否<扇形半径，若是进入第2步
- 判断u与ot之前的夹角θt是否<θ,方法如下：
因为cosθ在[0,π]区间单调递减，如下图所示：
所以只需要判断cosθt > costθ即可。u点和t点的坐标是已知的，因此根据点积公式很容易求出cosθt、cosθ。
参考：https://blog.csdn.net/kebu12345678/article/details/80724336
参考：https://blog.csdn.net/u012175089/article/details/50850250
参考：https://www.cnblogs.com/miloyip/archive/2013/04/19/3029852.html
参考：https://wuzhiwei.net/vector_in_games/
参考：https://www.gameres.com/493846.html