JPS算法本质上是对A* 算法的优化,在大部分情况下比传统A* 算法快上百倍。通过性能统计可以现,A* 算法大量时间都花在操作openset和closedset上,其原因就是加入openset的节点太多。JPS只会把关键的节点(跳点)加入openset中,从而大大减少了维护最小堆的开销。
一、概念
JPS在传统A* 算法基础上提出了强迫邻居和跳点的概念,这是减少openset中格子数量的关键。
1.1 强迫邻居
直线方向搜索:直线方向搜索存在两种方案,忽略对角线阻档和不忽略对角线阻档,根据实际需求选择一种。
忽略阻档:当前格子的左邻居为阻档且左前邻居为非阻档,则左前邻居为强迫邻居(紫色格子),当前节点为跳点(绿色格子);同理若理当前格子的右邻居为阻档,右前邻居为非阻档,则右前邻居为强迫邻居,当前节点为跳点。如下图所示
不忽略阻档:当前格子左邻居为非阻档且左后方为阻档,则左邻居为强迫邻居,当前节点为跳点;同理若当前格子右邻居为非阻档,右后方为阻档,则右方邻居为强迫邻居,当前节点为跳点。(上图中X为跳点)
对角线方向搜索:
当前格子左邻居为阻档且左上方为非阻档,则左上方格子为强迫邻居(紫色格子),当前格子为跳点(绿色格子);同理当前格子下方为阻档,右下方为非阻档,则右下方格子为强迫邻居,当前格子为跳点。如下所示
1.2 跳点
- 如果parent(x)到x是沿对角线移动,x可以通过水平或垂直方向移动到跳点j,则x也是跳点。(如果遇到此情况,应该把x加入openset, j暂时不加入。因为如果f(j) < f(x)的话,下次从openset取出f值最小的格子可能是j,而从parent(x)不一定能直接移动f(j),必须先走到x)
- 如果节点x有强迫邻居,则x节点为跳点。
- 起点、终点都是跳点。
二、算法流程
- 首先把起点加入到openset。
- 从openset中取出F值最小的点作为当前节点并加入closedset,从当前节点开始沿直线(水平或垂直)方向搜索跳点,若找到跳点则停止该方向的搜索并把跳点加入到openset中,否则直到遇到地图边界或阻档停止当前方向的搜索。
- 从当前节点开始往对角线方向搜索跳点,对角线方向到达一个新格子后,优先搜索该格子的水平分量方向,找到跳点则加入openset, 遇到边界或阻档停止当前方向搜索;再搜索垂直分量。对角线方向的搜索直到遇到跳点、边界、阻档停止。
- 如果当前格子的(8个方向)水平、垂直、对角线方向都搜索完毕,则本轮搜索结束。
- 重复步骤2、3、4直到找到终点。
三、寻路实例
下面通过一个例子来看下JPS算法寻路的整个过程,在图中,绿色格子为起点,红色格子为终点,灰色格子为路径上的跳点,紫色为加入openset,但没有成为路径点的跳点。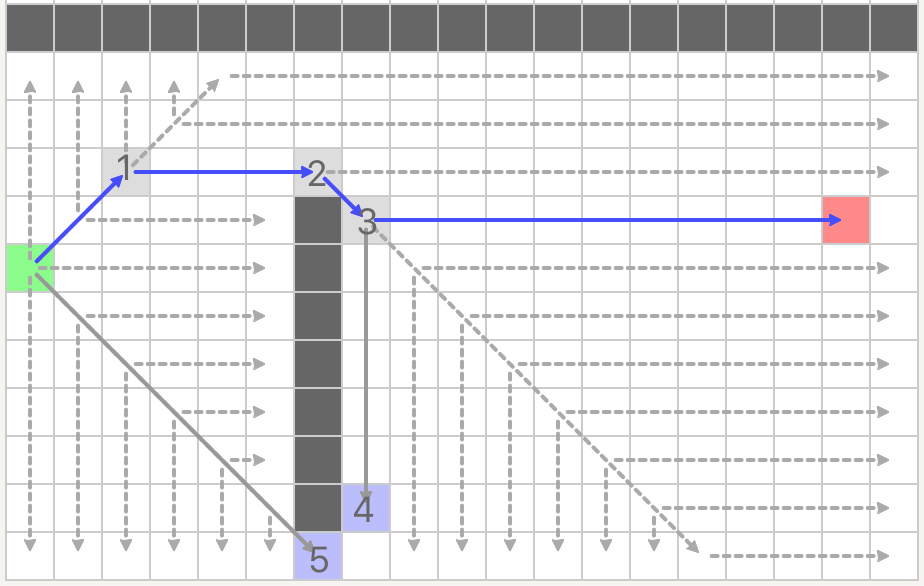
- 把起点加入openset,从openset中取出F值最小的格子,从openset中删除,加入closedset中。因为是起点没有方向,所以从当前格子8个方向寻找跳点(根据规则,直线和对角线方向都可搜索时,优先搜索直线方向)。
- 直线方向搜索时右边、顶部都遇到阻档,底部遇到边界,本次停止这3个方向的搜索。
- 开始对角线方向搜索,在右下对角线方向所有格子及其分量上遇到跳点(格子5),加入到openset,并停止该方向的搜索。
- 向右上对角线搜索时,在格子1处水平方分量搜索时,遇到格子2为跳点(根据规则:右邻居为阻档,右上为非阻档),因为起点到格子1为对角线方向,根据跳点规则1,格子1也是跳点。
- 把格子1加入到openset,此时,本轮搜索完成。现在openset中有2个跳点,格子5和格子1,从中取出F值最小的格子1,以格子1为当前格子继续搜索。
- 水平方向搜索时,发现跳点(格子2), 加入openlist, 并停止该方向的搜索。垂直、对角线方向都遇到阻档停止该方向的搜索。本轮搜索结束。现在openset中有格子5、格子2,从中找出F值最小的格子2,从openset中删除,加入到closedset中。
- 以格子2为当前格子继续搜索,水平方向遇到边界停止。
- 对角线方向搜索第1步时,水平分量遇到跳点为终点(根据跳点规则3:起点、终点都是跳点),加入openset。垂直分量遇到跳点(格子4:右邻居为阻档,右上为非阻档)加入openset。
- 虽然终点已经加入openset,但按照规则,本轮搜索仍未结束。继沿对角线及其水平垂直分量搜索,在本例中,它们都遇到边界而结束。
- 从openset中取出F值最小的格子,这里是终点,此时搜索结束。路径为点起->格子1->格子2->格子3->终点。
四、优化
1.1 两点是否可达
游戏地图中,并非所有格子之间都是连通(可达)的,如下图所示,区域S和区域E之间是不可达,如果我们不对地图预处理,那么玩家每次尝试从区域S到区域E我们都会寻一次路才知道是否可达,这显然不科学,因为只有在两点可达时才有寻路的必要。通常地图中出现点之间不可达(两点为非阻档)是策划配错了,因此我们可以把不可达的信息提前告知策划。
地图上的格子可以看成是非连通图,利用图的广度优先算法来遍历区域内的格子并对其编号,所有连通的格子编号相同。寻路时先判断起点与终点的区域编号是否相同,相同则可达,否则不可达。方法如下:
遍历地图上的所有格子,并作如下操作:
- num(区域编号)+ 1
- 如果当前格子是阻档或已访问过的,则跳过。
- 利用广度优搜索算法遍历当前格子四个邻居,并把当前格子及其邻居标记为已访问过,域编号设为num.
- 重复执行1 ~ 3步,直到地图所有格子都被访问过。
1.2 剪枝算法
对角线搜索时可能遇到一些中间跳点,这们只有承接作用,不具备扩展作用,加入openset会增加扩展次数,因此我们在搜索时不需要把它们加入openset,只需要把它们后继节点的parent设置为当前跳点的parent即可。下面我们通过一个例子来看下剪枝细节。(这里只讨论对角线方向,直线方向同理)
1.2.1 不剪枝的搜索流程
- 把起点0加入openset, 从openset移除F值最小的格子,加入到closedset。
- 继续搜索格子0的水平方向(遇到跳点)、垂直方向(遇到边界)、对角线方向(遇到跳点),并把跳点1、10加入openset。
- 从openset中删除F值最小的格子(格子1),加入closedset,把格子1作为当前节点继续搜索。
- 重复步骤2、3,直至此搜索完成。
最终路径为:0、1、2、3、4、5、6
1.2.2 剪枝搜索流程:
- 把起点0加入openset, 从openset移除F值最小的格子,加入到closedset。
- 搜索格子0的水平方向(遇到跳点10)、垂直方向(遇到边界)、对角线方向(遇到跳点1),把格子10加入openset,因为格子1是格子0对角线方向的节点(中间节点),不加入openset。
- 搜索格子1的水平(遇到跳点9)、垂直(遇到边界)、对角线(遇到跳点2)方向,把格子9的parent设置为格子1的parent(格子0)。格子2是格子1对角线方向的节点(中间节点),不加入openset。
- 继续沿对角线方向搜索直至完成。
搜索结束后,current为格子0,从openlist中出取F值最小的格子6,此时路径为:0,6。从图上可以看出格子0到格子6不能通过直线到达。因此我们需要在这两个格子之间插入拐点。
1.2.3 拐点插入规则
- 设剪枝后相邻两个跳点jp(i)、jp(i+1)的x、y坐标差的绝对值为(dx,dy),若dx或dy等于0,说明垂直或水平方向可达;若dx==dy说明对角线方向可达。不需要加入跳点。
- 如果dx,dy不相等,则需要加入中间拐点,拐点位置为,jp(i)沿对角线方向走min(dx,dy)。
根据拐点添加规则,本例中我们在跳点1,6之间加入跳点5,所以最终路径为:0,5,6。
1.3 路径优化
有时两点之间本可以走直线的,但根据JPS的寻路特性,可能在两点间加入”多余”的拐点,我们希望的是尽量走直线。如下图所示:
从起点出发(绿色格子),对角线搜索到灰格子处时,沿水平分量搜索遇到跳点(红色,即终点),由跳点定义1可知,灰色格子也是跳点。最终路径为:绿色格子、灰色格子、红色格子。从图中可以看出,从起点到终点是可以走直线的,但JPS找出的路径却多了中间节点,这在游戏中的表现可能比较诡异。因此我们需要优化JPS搜索到的路径,方法如下:
假如:JPS得到的路径为 A、B、C、D、E、F、G。我们需要判断,A到C是否直线可达,如果可达;继续判断A到D是否可达,如果不可达,则删除路径点B,当前路径点为A、C、D、E、F、G。继续判断C到E是否可以,以此类推直到终点。
那么如何判断两格子之间是否直线可达呢?
这里可以通过bresenham算法判断,如果直线上有格子是阻档,则不可达,否则可达。
参考
腾讯游戏开发精粹
https://zerowidth.com/2013/a-visual-explanation-of-jump-point-search.html