本文介绍3种游戏开发中常见形状间的碰撞检测方法。坐标原点均为左下角。
一、矩形物体间的碰撞检测
矩形之间的碰撞检测方法有很多,比如:
方法1可以通过点与直线的关系求得,方法2可以通过向量叉乘求得。下面介绍通过坐标方式来求两个矩形的交点。
原理:
排除两个矩形在水平方向和垂直方向不相交的情况,其余情况均为相交。
1.1 水平方向
B.max(x) < A.min(x) 或 B.min(x) > A.max(x) 则水平方向上不相交,如下图所示
1.2 垂直方向
B.max(y) < A.min(y) 或 B.min(y) > A.max(y) 则垂直方向上不相交,如下图所示
二、矩形与圆形的碰撞检测
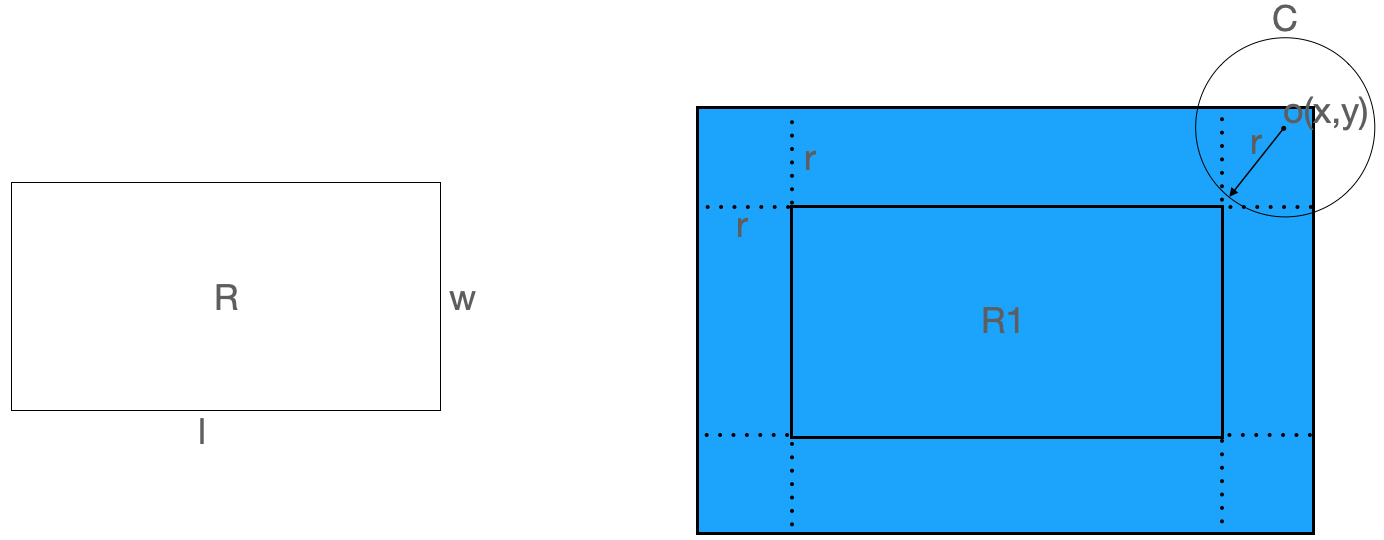
假设矩形R的长为l宽为w,圆C的圆心为o(x,y),半径为r。把矩形的长、宽分别向外扩张长度r得到新的矩形R1。
1.1 只要圆心在R1外则可以认为R与C不相交
1.2 若o在R1内:分两种情况:
- 情况1:o在R1的左上、左下、右上、右下四个角的矩形(简称顶点矩形)中,则需判断当前顶点是否在圆内,若在圆内则相交,反之不相交。
- 情况2:若o不在顶点矩形内,则圆与矩形相交。
还有另一种更简单的方法检查圆与矩形的碰撞:对于圆形可以取其包围矩形来计算,这样就变成了矩形与矩形之间的碰撞。缺点是不够准确。
三、扇形物体与圆形的碰撞检测
扇形与圆形相交大概分为3种情况:
1.1 扇形圆心在圆内:扇形圆心到圆的圆心距离 < 圆的半径
1.2 圆的圆心在扇形的向量之间
若圆半径+扇形半径 < 两圆心之间的距离则相交。可以通过点与直线关系判断圆的圆心是否在两向量之间。下图所示:只需要判断点c是否在l1右边、l2左边即可。
1.3 扇形任意一条边与圆相交:求直线与圆是否相交既可。方法

参考:《游戏开发的数学和物理》